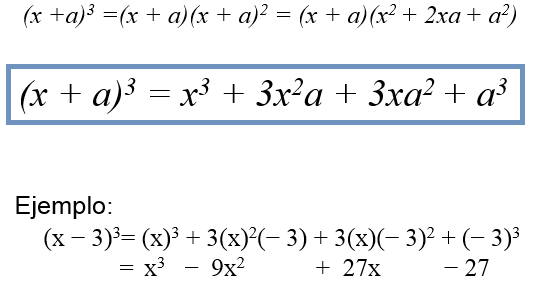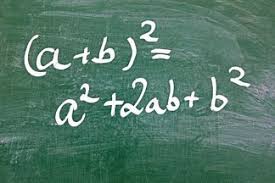Repaso de Álgebra
Expresiones algebraicas y las operaciones con ellas
Las expresiones algebraicas están compuestas por términos (o monomios) separados por signos de suma o resta, éstos contienen factores numéricos llamados coeficientes y factores no numéricos o letras, que en general representan variables, llamado parte literal.
Si los factores literales se encuentran elevados a un exponente entero positivo las expresiones de denominan polinomios. El grado del término será el del mayor exponente.
En realidad cada término o monomio, implica una multiplicación, es decir el producto de los factores que componen la expresión por ejemplo el monomio 2x^3 = 2* x * x * x, o también = (x * x * x )+ (x * x * x) (dos veces «x» al cubo).
Ejemplos de expresiones algebraicas:
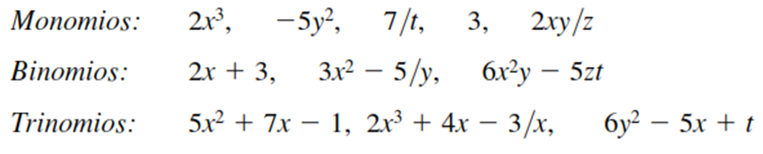
Operaciones algebraicas
1. Adición y sustracción de expresiones
Sólo se pueden sumar (o restar) los términos semejantes, es decir cuyas partes literales sean iguales (mismas variables elevadas a la misma potencia). Simplemente sumando los coeficientes numéricos.
Esto es así ya que si factorizamos la expresión, podemos ver claramente por qué solo operamos la parte numérica solamente.
Ejemplo 1: 4x +3x = (4+3)x = 7x
Los términos 3x y 4x son semejantes por contener ambos la variable x elevada a su primera potencia. El hecho de que sus coeficientes (3 y 4) sean diferentes no influye en la semejanza de los términos. Cuando se suman o restan polinomios, pueden combinarse términos (los semejantes) y obtenerse así una forma más simple (7x en el ejemplo).
Ejemplo 2: 5xy − 2xy + 6xy = [5 +(− 2) +6]xy = 9xy
Los términos que no son semejantes no pueden combinarse para dar un término individual.
Así, los términos en esta otra expresión 2x + 5xy no pueden expresarse en un solo término reducido (no pueden combinarse).
Procedimiento general
Para facilitar la suma de expresiones algebraicas, conviene reagrupar los términos de tal manera que las expresiones que sean semejantes aparezcan juntas.

2. Multiplicación de expresiones algebraicas
Al multiplicar expresiones de varios términos entre si es útil, para aplicar la propiedad distributiva, usar el método de los arcos para multiplicar cada término de la primer expresión por cada monomio de la segunda.
Por ejemplo para realizar la multiplicación (x+2)(y+3):
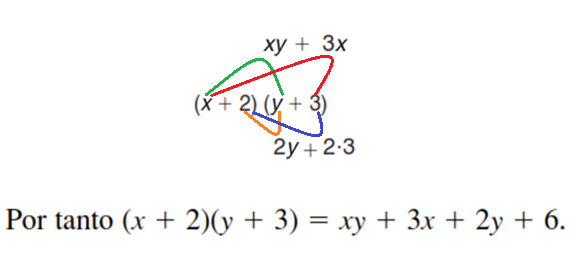
Productos especiales o "productos notables"
Existen ciertos tipos de multiplicaciones de estas expresiones o productos especiales que aparecen con tanta frecuencia que pueden manejarse como fórmulas estándar:
1. Producto de binomios con un término común «x»: (x + a)(x + b)
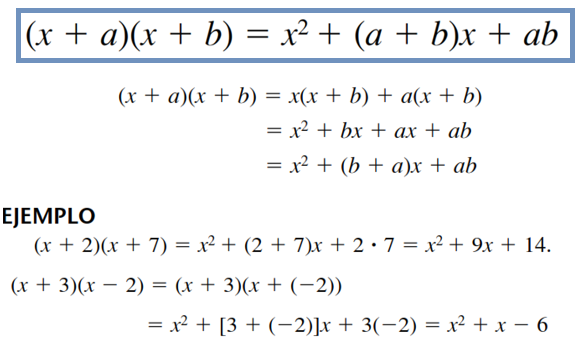
2. Binomio al cuadrado: (x + a)(x + a)
La fórmula es similar a la anterior pero reemplazando el término «b» del segundo binomio por «a».
El cuadrado de la suma (o diferencia) de dos términos es igual a la suma de los cuadrados de los dos términos más el doble de su producto.(“cuadrado del primero + doble del primero por el segundo + cuadrado del segundo”)
En la fórmula quedaría así:
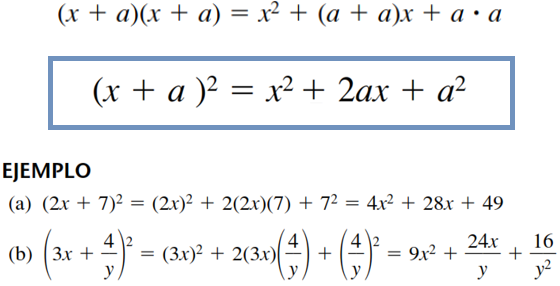
3. Producto de binomios conjugados: suma por diferencia de términos
El producto entre la suma y la diferencia de dos términos (binomios conjugados) es la diferencia de los cuadrados de los dos términos.
En la fórmula quedaría así:
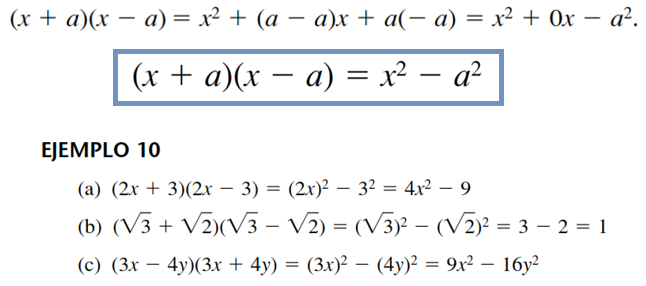
4. Cubo de un binomio:
El cubo de un binomio = al cubo del primer término + el triple del primer término al cuadrado, por el segundo + el triple del primer término, por el segundo al cuadrado + el triple del segundo término.
En formula: