Función Inversa
1. Definición de Función..
Función Inversa Cálculo 1b Fcea-Udelar:
Este tema es parte de la preparación de la asignatura Cálculo 1 (1b) de la Facultad de ciencias Económicas y Administrativas de la Universidad de la República (Fcea-Udelar).
Una función es una relación entre los elementos de un conjunto A (conjunto de entradas o dominio) y los elementos de un conjunto B (conjunto de salidas o Codominio), en la cual cada elemento de A tiene uno y solo un correspondiente en B.
Las funciones son muy importantes en las ciencias y en la vida práctica, ya que se utilizan como herramienta para modelar un fenómeno que se quiere estudiar.
Fenómenos como el comportamiento esperado del consumidor cuando cambia el precio de un bien, para estimar el ritmo de contagio de una epidemia, para calcular el material de una construcción o el cableado en un tendido eléctrico.
Una función es, en la práctica, una operación que transforma el valor numérico de una variable (variable independiente) en un valor numérico de otra (variable dependiente).
Ambas variables pueden pertenecer al campo de los números reales, los enteros, etc. Cuando una función f transforma números reales en otros números reales, y se denota f : R → R.
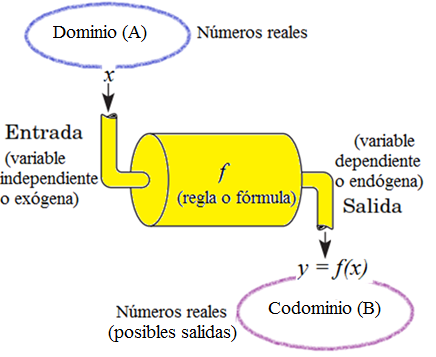
Dominio: valores que toma la variable independiente para los que tiene sentido el cálculo del valor de la variable dependiente.
En algunas funciones existen ciertas operaciones donde el conjunto R no es cerrado, y es imposible calcular el valor funcional en esos casos.
Como f(x)=√x con sentido para x ≥0, así el dominio de la función f es el conjunto {x/x ∈R, x ≥ 0} .
Codominio e Imagen: el codominio corresponde a los valores que puede asumir la variable dependiente al aplicarse el operador funcional, la imagen son los valores que realmente asume la función.
Resumiendo:

Funciones Inyectivas ...

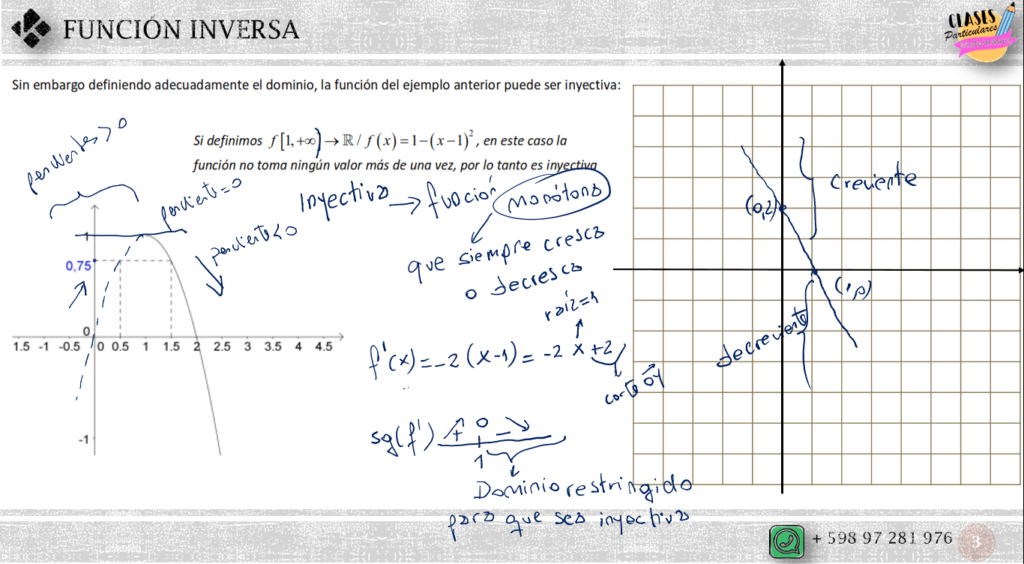
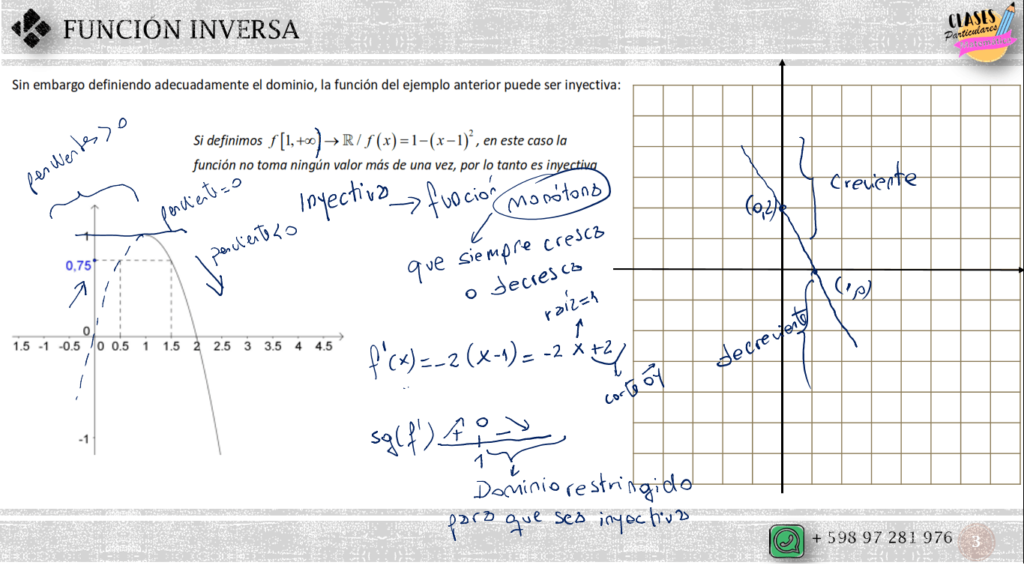
A continuación se presenta la función anterior, cuadrática de coeficiente principal negativo y por lo tanto de concavidad negativa, evidentemente no inyectiva ni sobreyectiva.
Si se redefine en primer lugar el dominio para así convertirla en inyectiva, posteriormente se redefine el dominio para que, coincidiendo con el recorrido sea sobreyectiva, la función será biyectiva y por lo tanto invertible.
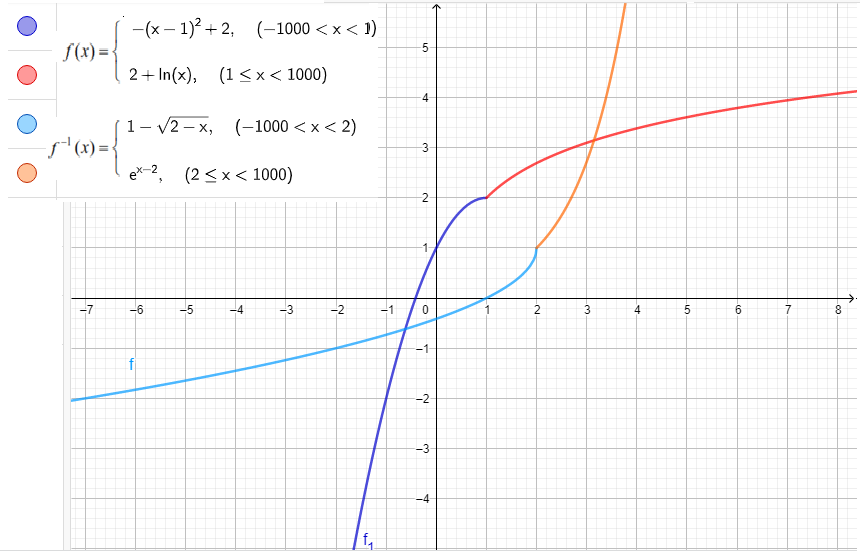
Función Inversa ... ejercicio de ejemplo...
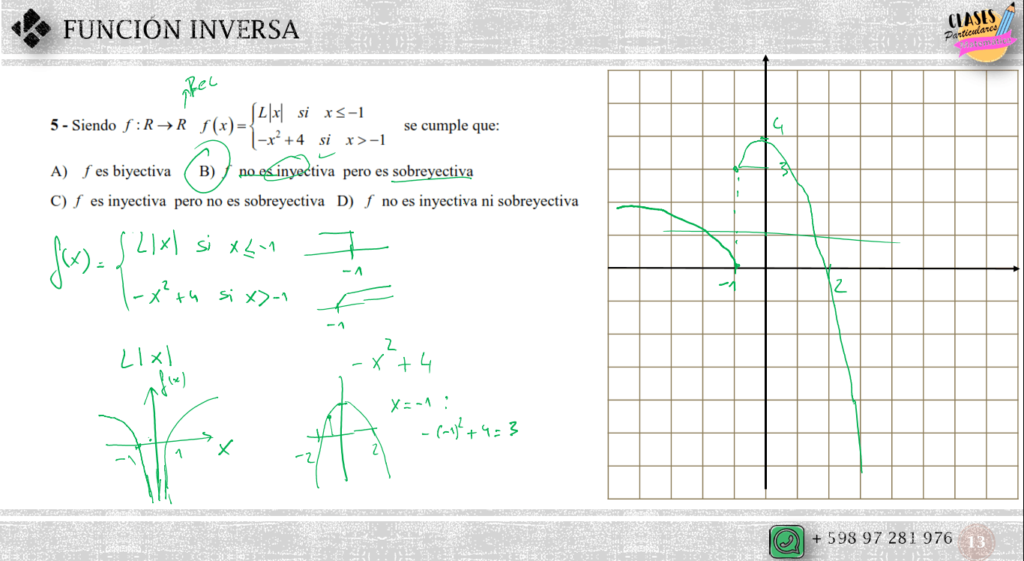
En el siguiente ejercicio de ejemplo, tomado de un examen de cálculo de la Udelar, te muestro como se determina una inversa a partir de una función del tipo «por partes»* o «tramos», redefiniendo el su codominio para que coincida con el recorrido, característica de una función biyectiva, tipo necesario para la existencia de invertibilidad.