Cómo despejar una variable
Ecuaciones de primer grado con una incógnita
El término ecuación significa igualdad. En general, toda ecuación de una variable puede ser reducida a la forma:
f(0) = x, siendo f: R →R :
Dado que x es variable, la igualdad se presentará para algún(os) valores de x .
Métodos para hallar el (los) valor(es) de x que verifican la igualdad:
La suma de una constante o una variable en ambos lados de la ecuación no afecta el equilibrio de la misma. Este concepto también es extensible a la resta, división y multiplicación. Por ejemplo, sea la ecuación:
a + d = b + c, la ecuación no se altera si a ambos lados de la igualdad se les suma la constante − b, quedando la ecuación entonces:
a + d − b = b + c − b
es decir: a + d − b = c
Aquí, como se puede apreciar, se ha despejado c, que es la variable que queda «sola» de un lado del signo «=». Normalmente, por convención o costumbre, la variable despejada suele ubicarse a la izquierda del «=», aunque dá lo mismo que esté a un lado u otro.
Ecuación de tipo ax+b=0
Si una ecuación puede expresarse en la forma ax + b = 0 , recibe el nombre de ecuación de primer grado con una incógnita.
Como a y b son constantes conocidas, siempre existe algún valor de la variable x que logra cumplir la igualdad.
Aplicando el procedimiento anterior, en caso de sumar −b en ambos lados de la ecuación, se obtiene:
ax + b −b = 0 −b
es decir: ax = −b
Multiplicar por una constante a ambos lados de la ecuación tampoco afecta el balance de la misma, por lo tanto, multiplicando por la constante 1/a se obtiene:
(1/a) ax=-b (1/a)
Resultando: x=-b/a
Siendo -b/a el valor de x que permite resolver la ecuación.
Esta es la solución general de toda ecuación de primer grado de una sola variable.
Ecuación de la recta: ax + b = y
Las expresiones anteriores se pueden generalizar con la expresión ax + b = y, pudiendo interpretar los resultados en una gráfica.
Sea el conjunto A={(x,y), x,y ∈ R/ ax + b= y}.
El conjunto está conformado por infinitas duplas, y puede representarse en el plano cartesiano mediante una recta.
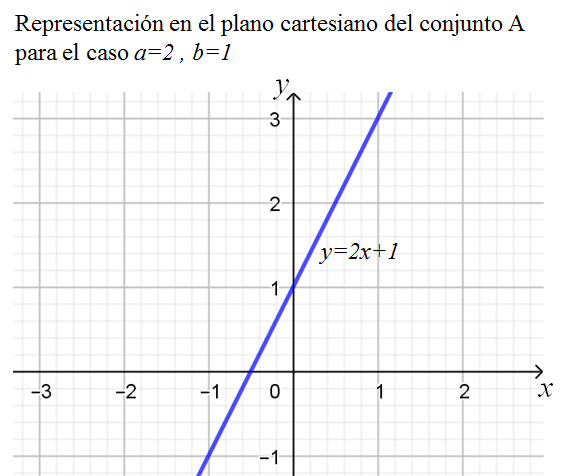
Raíz de la recta:
y=0, x= −b/a; punto del plano (−b/a, 0)
Ordenada al origen:
x=0, y=b; punto del plano (0, b)
En la gráfica la recta formada por la representación de las duplas pertenecientes al conjunto A, intersectan el eje de las abscisas en el valor x=−½, conocido como raíz, valor para el cual y=0; también el valor de y cuando x=0, y=b (ordenada al origen)
En la gráfica la recta formada por la representación de las duplas pertenecientes al conjunto A, intersectan el eje de las abscisas en el valor x=−½, conocido como raíz, valor para el cual y=0; también el valor de y cuando x=0, y=b (ordenada al origen)
Raíz
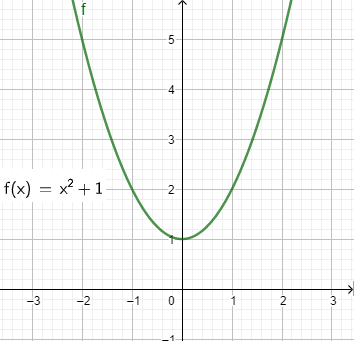
El concepto de raíz no solo se aplica a la ecuación de la recta, es extensible a cualquier tipo de función, aunque no toda función f:R →R tiene raíces. Por ej. la función f(x)= x² + 1 nunca =0, en el dominio de R y su gráfica no presentará intersección con el eje de las abscisas.
Ecuación de segundo grado con una incógnita
Si una ecuación puede expresarse en la forma ax²+bx+c=0, recibe el nombre de ecuación de segundo grado con una incógnita, en su forma completa general.
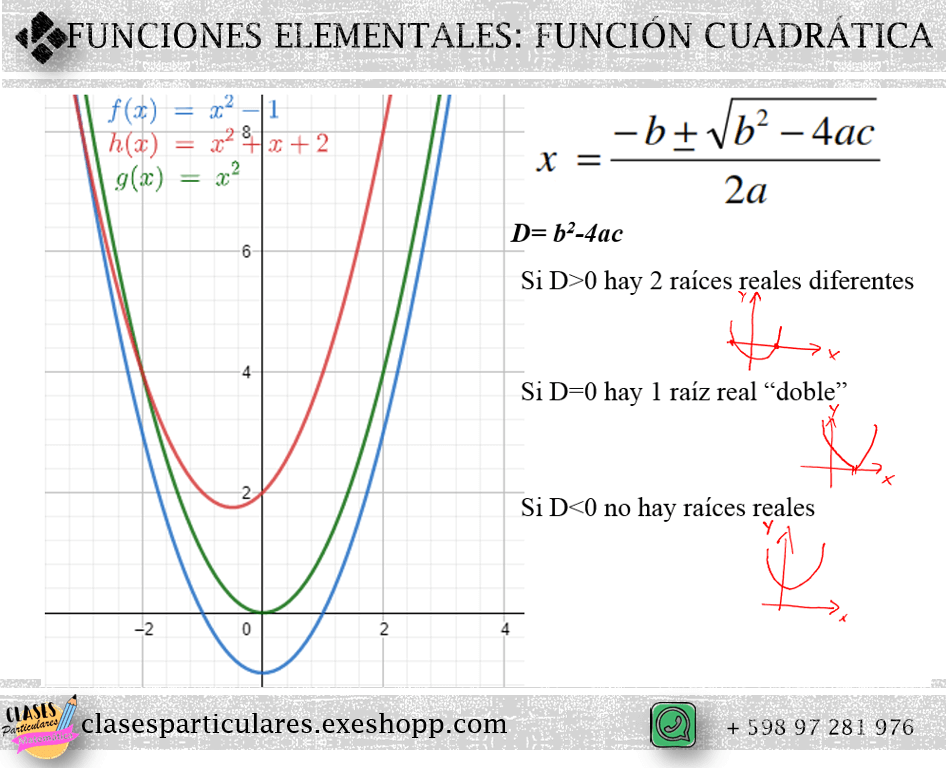
En este caso para calcular las raíces, en caso de contar con ellas se utiliza la fórmula cuadrática:
x=(-b±√(b²-4ac))/2a
La representación en el plano cartesiano del conjunto de duplas:
{(x,y), x,y ∈ R/ y = ax² + bx + c}, es una parábola (cónica).
La expresión b²-4ac , el subradical de la fórmula cuadrática, llamado discriminante (D) de la ecuación de segundo grado y es quien determina cómo son las raíces del polinomio P(x)=ax²+bx+c, es decir, los puntos de corte de la parábola con el eje de las abscisas.
El valor de D puede ser clasificado en tres categorías: D>0 , D= 0 o D<0, obteniendo así como resultados, dos raíces distintas; una raíz doble; y sin raíces reales (o con raíces complejas) en el último caso.
Coordina tus clases particulares presenciales o virtuales (por hora) haciendo click en el globo de WathsApp o en la imagen de abajo. Puede ser una sola clase de consulta.
